where sideal represents the bond-valence contribution from a single bond that would give rise to a total valence sum V(A) = Videal(A).
In Fig. 1 it is presumed that a monovalent central cation A+ is
symmetrically coordinated by four anions X z-. Assuming that only
nearest neighbours contribute to the valence sum the ideal bond-valence
contribution from a single bond would thus be
s(ideal,A-X)
= ¼. Any deviation of the bond length RA-X
from its ideal value Rideal (corresponding
to sideal) leads to an increase of |sA-X
| = |sA-X
- sideal|. The concavity
of the relation between s and R ensures that the increase
of
|sA-X|
is steeper
in the R < Rideal branch. For a given coordination
type the postulation of a fixed value of b in this picture would
mean that the shape of the pseudopotential becomes identical for all monovalent
cations (cf. broken line in Fig. 1), irrespective of the type of bonding
or the polarizability of the interacting particles. Thus, applications
of the bond-valence concept to any field that might be affected by the
shape of the bond-length bond-valence pseudopotential should not rely on
bond-valence parameter sets with a fixed parameter b. It appears
more natural to incorporate the effects of the polarizability by the determination
of a suitable value of b
instead of treating it as a correction
term to the atomic radii [as had been performed implicitly in (4)].
 |
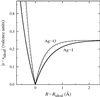Figure 1 (from ADAMS,
Acta Cryst. B 57, 278-87 (2001).
Pseudopotential representation of the correlation between bond-length R and bond valence s. Rideal is the bond distance that leads to a bond valence of sideal = 0.25 v.u. (the bond valence for a monovalent cation in a symmetrical tetrahedral coordination). Full lines refer to bond-valence parameters of Ag-O and Ag-I with freely refined b (Radaev et al., 1994; Trömel, 1994); the broken line displays the universal shape for pseudopotentials that employ a fixed b = 0.37 Å. |
Adjusting the value of b to the softness of a bond at first requires
an independent measure of the softness of a bond. Following Parr &
Pearson (1983) individual atoms, ions or radicals may be characterized
by their `electronic chemical potential' 
and their `absolute hardness' 
.
The exact definition of these quantities as
and 
where N equals the number of electrons and 
represents the potential of the nucleus and external influences, may appear
quite abstract, but for neutral particles approximate values for
and are experimentally
accessible from the relation of these quantities to ionization energy IE
and electron affinity EA
In this approximation || becomes
identical to Mulliken's definition of the absolute electronegativity 
abs.
It should be noted that for a system in equilibrium abs attains a constant site-independent value, whereas the value of
varies locally with a global average value of
is thereby defined as the reciprocal value of hardness .
The softness of a cation M z+ may be calculated in the same manner
using the ionization energy of M z+ as IE (= "(z+1)th ionization
energy") and replacing EA by the ionization energy of M(z - 1)+ (Pearson,
1985).
As electron affinities of anions are generally inaccessible (and their meaningfulness in the determination of bond softnesses appears questionable), a similar extension to anions is not viable. According to Pearson (1988) the values of IE and EA for the neutral elements may serve as a rough approximation for the anions. In the first part of the paper we will follow this guideline. Later it will be outlined how an empirical correlation between the anion radius and the anion softness may be utilized to obtain a more precise estimate of the anion softness. To derive a measure for the softness of the A-X bond, the softnesses of the interacting species A+ and X z- need to be combined.
In an earlier investigation on a possible connection between bond softness and bond valence, Urusov (1995) had argued that the softness of a bond should increase with the sum of the softnesses of the interacting particles. Contrasting to this assumption, the empirical HSAB (hard and soft acids and bases) concept (Pearson, 1963; Parr & Pearson, 1983; Nalewajski, 1993) suggests that reactions will occur most readily between species that match each other in hardness or softness. If the formation of strong bonds between anions and cations of equal softness is the fundamental reason for this empirical rule, then it appears straightforward to conclude that the interatomic potentials for these bonds should be steeper (and thus correspond to a smaller value of b) than those for the weaker bonds between particles of mismatched softnesses.
The diagrams in Fig. 2 compare the significance of the two suggested
correlations based on those literature bond-valence parameters (for halide
and chalcogenide compounds) that did not follow the assumption of a universal
bond-valence parameter b. Obviously there is no strong correlation
to be expected, since the comparison includes data from different sources
(some of them were rather old and therefore based on the considerably smaller
number of structures available at that time) using slightly different conventions
for the selection of `well determined' structures and the choice of the
counterions that contribute to the bond-valence sum. In some cases it is
also not evident whether the published b parameters were the results of
free refinements or biased, e.g. by whatever the authors assumed to be
`chemical knowledge'. Some of the bond-valence parameters are intended
to apply to atoms for a range of formal valences, but each valence state
corresponds to a different softness. The approximative conversion formula
suggested by Burdett & Hawthorne (1993) for parameter sets that employ
the power law ansatz of (2) systematically produces lower values of b.
The converted data have therefore been scaled by a constant factor of 1.25,
so that the average value of b for the literature parameter sets
from (1) and (2) becomes equal. Moreover, the exponent N of the
power law parameters was mostly given as an integer number in the literature,
which leads to noticeable rounding errors. Despite all these drawbacks
Fig. 2 reveals that the difference of the softnesses anion - cation should
be loosely related to b in the sense predicted by the HSAB concept, whereas
there seems to be no discernible correlation between b and
the sum of softnesses anion
+ cation.
From these data it is impossible to decide whether the slopes for the two
branches of the correlation between b and the softness difference
( anion
> cation
or anion
< cation)
differ, since the case anion anion
< cation
occurs only for a low number of cation-anion pairs. The apparent shift
of the minimum in the correlation to positive softness differences may
serve as an indication that the rough estimate of the anion softness (by
assuming equal softnesses for neutral atoms and anions) tends to overestimate
the anion softness.
 |
Figure 2 (from ADAMS,
Acta Cryst. B 57, 278-87 (2001).
Comparison of the dependence of the bond-valence parameters b on the difference between the softnesses of anions (halides and chalcogenides) and cations (left-hand side) or on the sum of these softnesses as predicted by Urusov (1995) (right-hand side). Large symbols refer to b values from various literature compilations (Radaev et al., 1994; Trömel,1994; Brown, 1981, 2000), while small symbols refer to b values converted from parameters of the power law ansatz of (2) as described in the text. In harmony with the HSAB concept, bonds between atoms with different softnesses tend to be weaker and therefore correspond to larger values of the parameter b (solid line: fourth-order polynomial fit to all data; broken lines: 99% confidence interval). However, no correlation at all is discernible in the right-hand side diagram between b and the softness sum for the same set of data. |
These findings do not preclude that a different combination of the individual softnesses might lead to a more significant correlation. In this context it may be noteworthy that Mohri (2000) recently derived an alternative formulation of the correlation between the bond distance and bond valence from a molecular orbital viewpoint. The conversion of his parameters into the conventional Brown-Altermatt formula leads to values of b that are generally lower (ca 2/3 of literature data), but exhibit the same rough correlation to the softness difference.
The low values of b found by Pauling (1947, 1960) in his early investigations of the analogous relationships between bond length and `bond order' for bonds between the same type of atoms (b = 0.30 Å for metals, b = 0.26 Å for C-C bonds) may be tentatively interpreted as a further line of evidence that bonds between particles of equal softness are characterized by a low value of b.